Primitives for computing the proximity measure between a source image and a template image. More...
Modules | |
| SqrDistanceFull_Norm | |
| Primitives for computing the normalized Euclidean distance between two images with full mode. | |
| SqrDistanceSame_Norm | |
| Primitives for computing the normalized Euclidean distance between two images with same mode. | |
| SqrDistanceValid_Norm | |
| Primitives for computing the normalized Euclidean distance between two images with valid mode. | |
| CrossCorrFull_Norm | |
| Primitives for computing the normalized cross correlation between two images with full mode. | |
| CrossCorrSame_Norm | |
| Primitives for computing the normalized cross correlation between two images with same mode. | |
| CrossCorrValid_Norm | |
| Primitives for computing the normalized cross correlation between two images with valid mode. | |
| CrossCorrValid | |
| Primitives for computing the cross correlation between two images with valid mode. | |
| CrossCorrFull_NormLevel | |
| Primitives for computing the normalized cross correlation coefficient between two images with full mode. | |
| CrossCorrSame_NormLevel | |
| Primitives for computing the normalized cross correlation coefficient between two images with same mode. | |
| CrossCorrValid_NormLevel | |
| Primitives for computing the normalized cross correlation coefficient between two images with valid mode. | |
Detailed Description
Primitives for computing the proximity measure between a source image and a template image.
General Introduction
There are basically two approaches to compute the proximity measure for template matching, Euclidean distance and the cross correlation.
- Euclidean distance computes the sum of the squared distance (SSD) between the corresponding pixels of the source image and the template image. The smaller the distance is, the more similar the source image and the template image is around the pixel. The anchor of the template image is used during the computations, which always lies in the gemotric center of the image. Given a source image
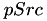 (
(  ) and a template image
) and a template image 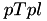 (
(  ), the Euclidean distance
), the Euclidean distance 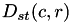 between two images at pixel in row
between two images at pixel in row 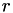 and column
and column 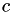 is computed as (
is computed as ( 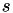 stands for source image and
stands for source image and 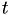 for template image for short):
for template image for short): ![\[D_{st}(c,r)=\sum_{j=0}^{H_t-1}\sum_{i=0}^{W_t-1}[pTpl(j,i)-pSrc(j+c-\frac{H_t}{2}, i+r-\frac{W_t}{2})]^2 \]](form_91.png)
- Cross correlation computes the sum of the product between the corresponding pixels of the source image and the template image. The cross correlation
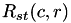 is calculated as:
is calculated as:
The larger the cross correlation value is, the more similar the source image and the template image is around the pixel.![\[R_{st}(c,r)=\sum_{j=0}^{H_t-1}\sum_{i=0}^{W_t-1}[pTpl(j,i)\cdot pSrc(j+c-\frac{H_t}{2}, i+r-\frac{W_t}{2})] \]](form_93.png)
- The cross correlation
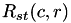 is affected by the brightness of the images which may vary due to the lighting and exposure conditions. Therefore, NPP computes the cross correlation coefficient to circumvent this dependence. This is typically done at every step by subtracting the mean from every pixel value, i.e.,
is affected by the brightness of the images which may vary due to the lighting and exposure conditions. Therefore, NPP computes the cross correlation coefficient to circumvent this dependence. This is typically done at every step by subtracting the mean from every pixel value, i.e., ![\[\tilde{R}_{st}(c,r)=\sum_{j=0}^{H_t-1}\sum_{i=0}^{W_t-1}[pTpl(j,i)-Mean_t]\cdot [pSrc(j+c-\frac{H_t}{2}, i+r-\frac{W_t}{2})-Mean_s] \]](form_94.png)
NPP computes the normalized values of Euclidean distance, cross correlation and the cross correlation coefficient.
- The normalized Euclidean distance
 is defined as:
is defined as: ![\[\sigma_{st}(c,r) = \frac{D_{st}(c,r)}{\sqrt{R_{ss}(c,r)\cdot R_{tt}(\frac{H_t}{2},\frac{W_t}{2})}} \]](form_96.png)
- The normalized cross correlation
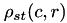 is defined as:
is defined as:
The![\[\rho_{st}(c,r) = \frac{R_{st}(c,r)}{\sqrt{R_{ss}(c,r)\cdot R_{tt}(\frac{H_t}{2},\frac{W_t}{2})}} \]](form_98.png)
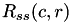 and
and 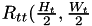 denote the auto correlation of the source image and the template image individually. They are defined as:
denote the auto correlation of the source image and the template image individually. They are defined as: ![\[R_{ss}(c,r)=\sum_{j=c-\frac{H_t}{2}}^{c+\frac{H_t}{2}}\sum_{i=r-\frac{W_t}{2}}^{r+\frac{W_t}{2}}pSrc(j, i) \]](form_101.png)
![\[R_{tt}(\frac{H_t}{2},\frac{W_t}{2})=\sum_{j=0}^{H_t-1}\sum_{i=0}^{W_t-1}pTpl(j,i) \]](form_102.png)
- Similarly, the normalized cross correlation coefficient
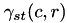 is calculated as:
is calculated as:
The![\[\gamma_{st}(c,r) = \frac{\tilde{R}_{st}(c,r)}{\sqrt{\tilde{R}_{ss}(c,r)\cdot \tilde{R}_{tt}(\frac{H_t}{2},\frac{W_t}{2})}} \]](form_104.png)
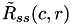 and
and 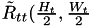 are defined as:
are defined as: ![\[\tilde{R}_{ss}(c,r)=\sum_{j=c-\frac{H_t}{2}}^{c+\frac{H_t}{2}}\sum_{i=r-\frac{W_t}{2}}^{r+\frac{W_t}{2}}[pSrc(j, i)-Mean_s] \]](form_107.png)
![\[\tilde{R}_{tt}(\frac{H_t}{2},\frac{W_t}{2})=\sum_{j=0}^{H_t-1}\sum_{i=0}^{W_t-1}[pTpl(j,i)-Mean_t] \]](form_108.png)
Categorizations
The Euclidean distance and the cross correlation are categorized into three types, full, same, and valid.
- Full mode indicates that the anchor of the template image starts from the outside of the source image, assuming the out-of-boundary pixels are zeor-padded. The size of the destination image is
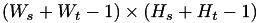 .
. - Same mode means that the anchor of the template image starts from the top left pixel of the source image. All the out-of-boundary pixels are also zero-padded. The size of the destination image is the same as the source one, i.e.,
 .
. - Valid mode indicates that there are no out-of-boudnary readings from the source image. The anchor of the template image starts from the inside of the source image. The size of the destination image is
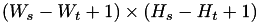 .
.